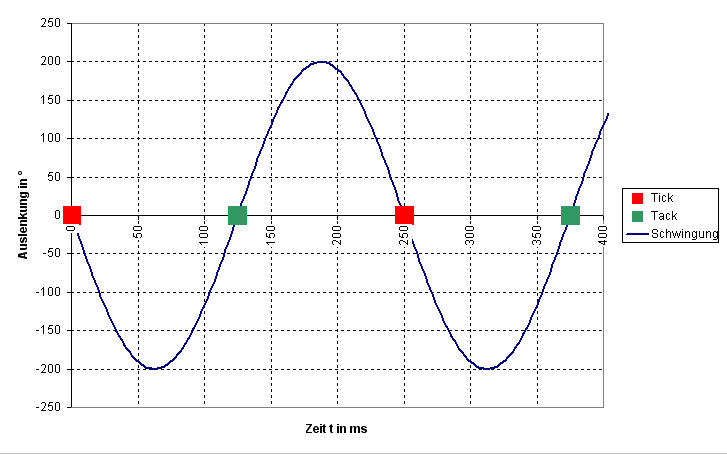
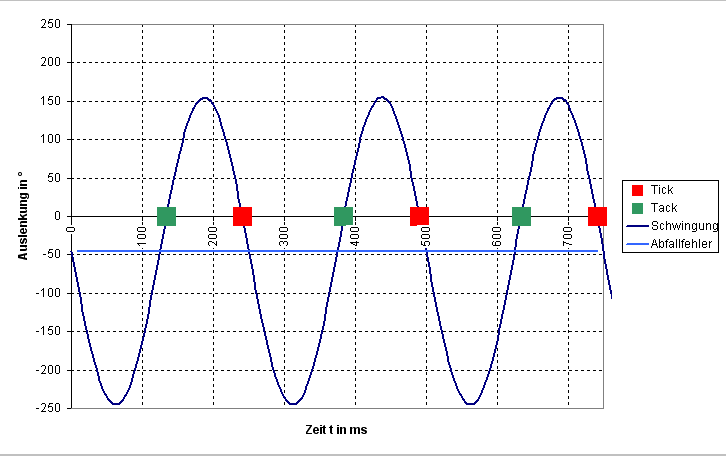
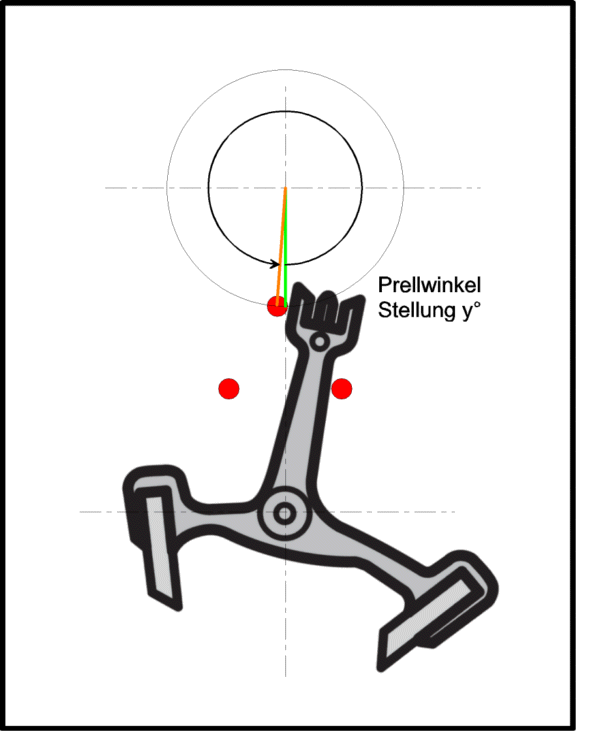
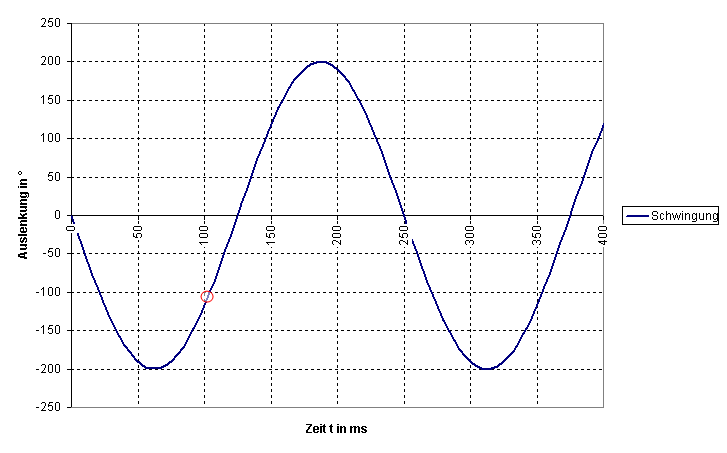
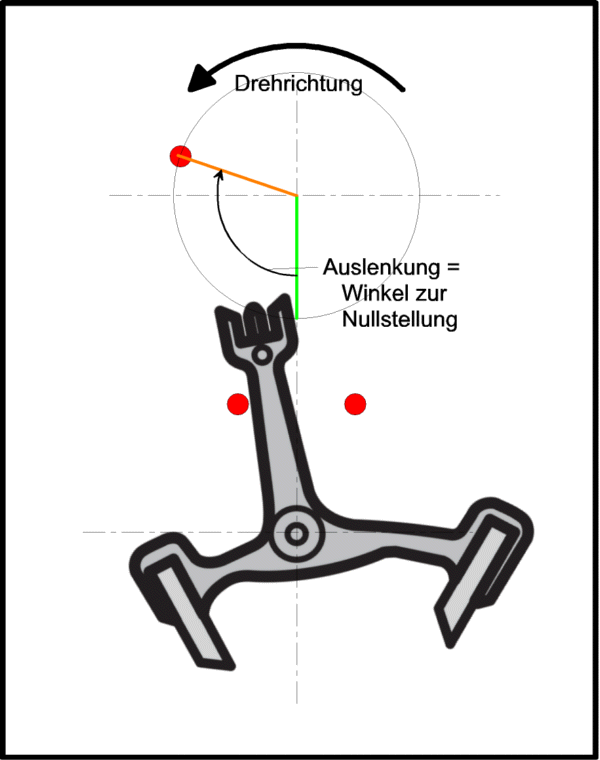
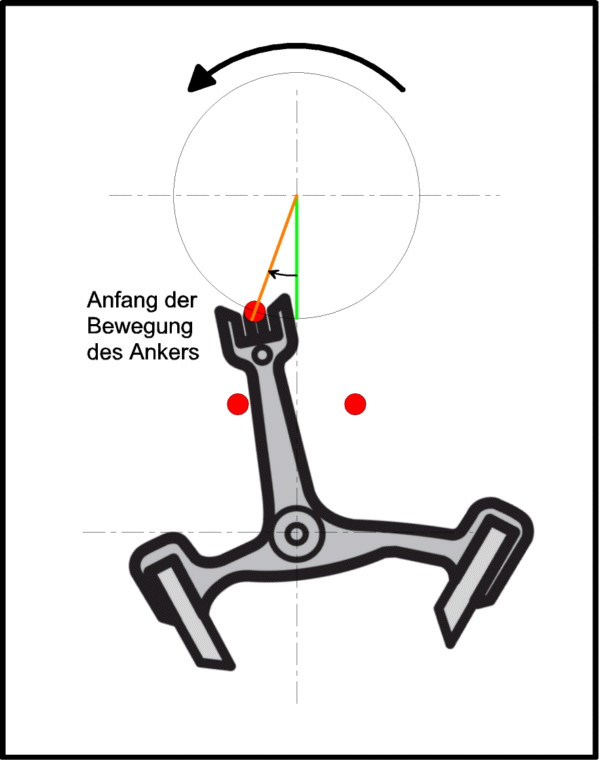
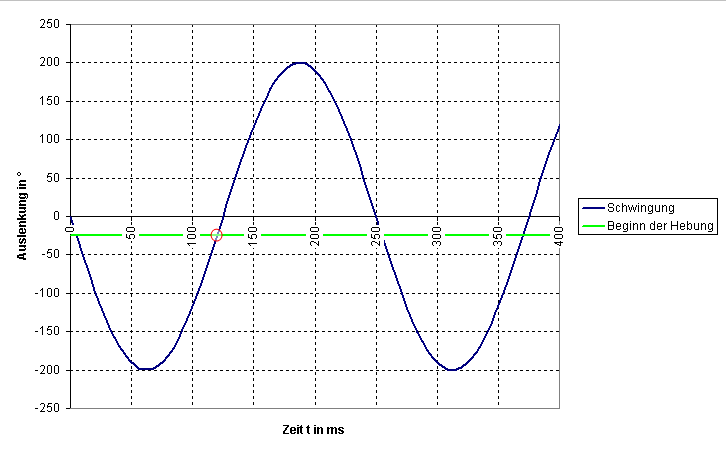
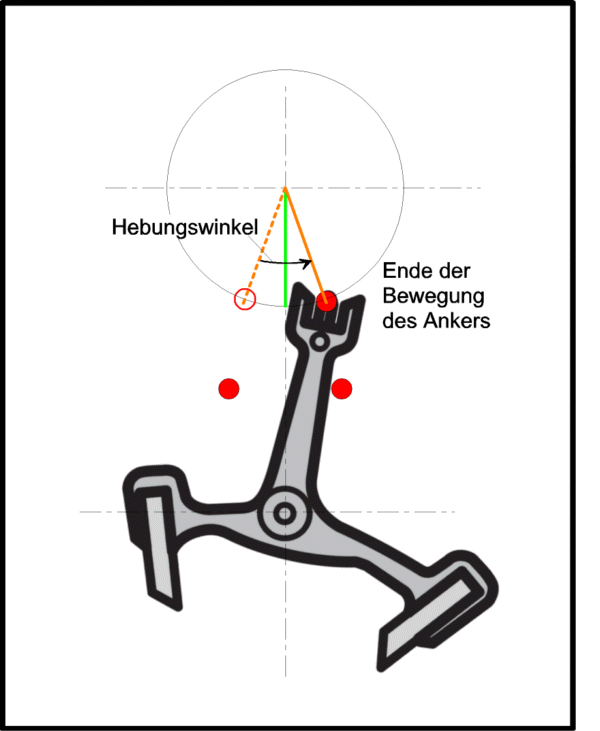
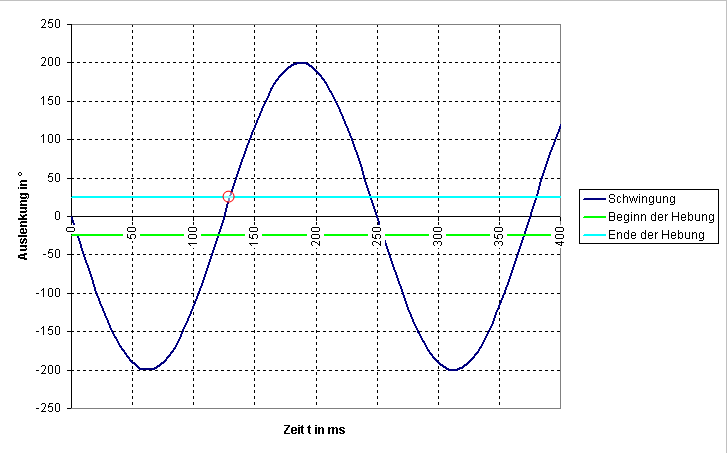
Jetzt kann man mit der Zeitwaage bestimmen, wie lange der >tick< dauert, die Zeitspanne vom ersten bis zum dritten Geräusch, von der Auslösung bis zum Fall.
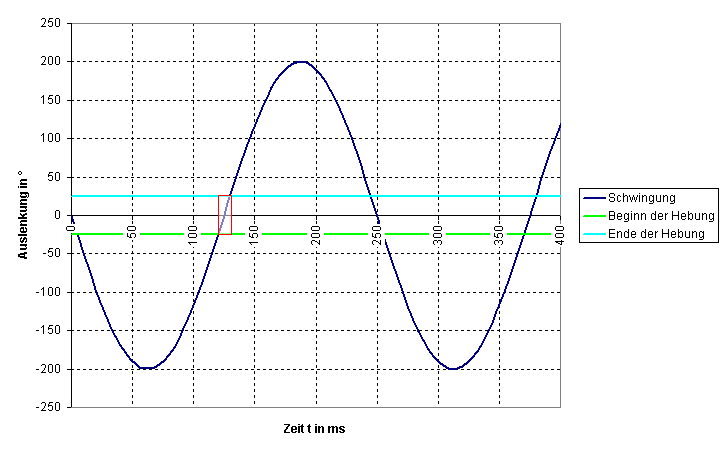
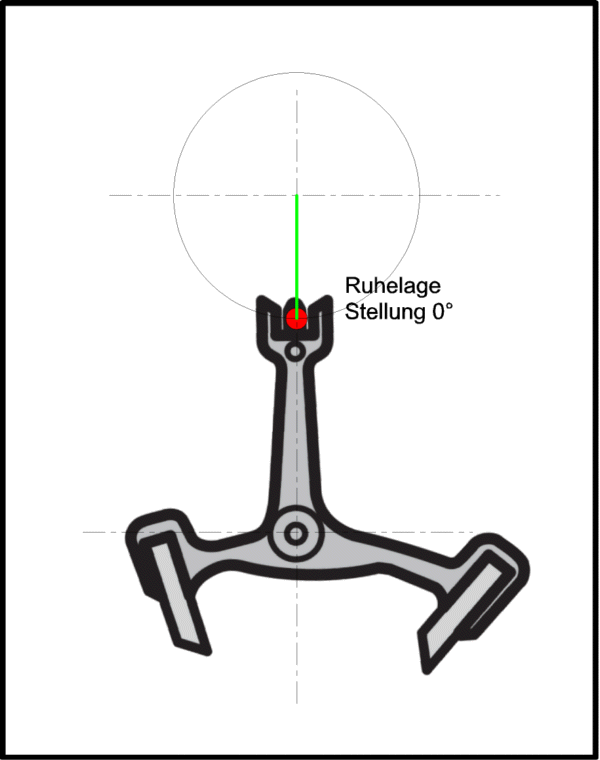
Im Beispieldiagramm sind es knapp 10 ms. Kennt man nun den Hebungswinkel des Kalibers, weiss man auch, wie hoch das rote Rechteck ist. Im Beispieldiagramm sinds 50°, ein ziemlich typischer Wert. Die (Winkel-)Geschwindigkeit im Nulldurchgang ist somit 50° in 10 ms oder aber 5000 °/s, schon ganz flott.
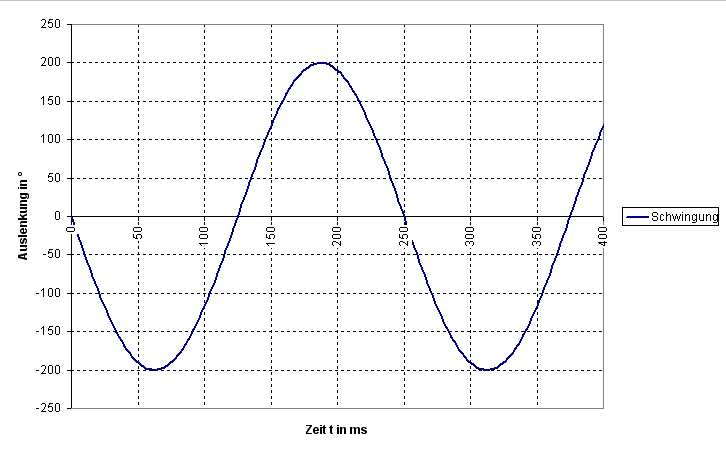
Das Problem ist, dass wir das eigentlich gar nicht wissen wollten, sondern die Amplitude. Wir wissen jetzt zwar die Steigung, aber nicht, wie hoch der Berg ist. Wie kommt man von der Steigung zur Höhe des Berges, das geht doch gar nicht? Geht doch, man braucht nur noch eine einzige zusätzliche Information. Im Grunde die, wie lange die Strecke ist. Die Steigung ist zwar nicht konstant, aber die Form ist bekannt, es ist eine harmonische Schwingung, auch als Sinusschwingung bekannt. Und wie lang die Schwingung dauert, das wissen wir ja schon von der Messung des Gangs!
Das Verhältnis von Amplitude zu Länge einer Schwingung ist proportional zur Steigung.
Klingt kompliziert, ist aber ganz einfach:
- Ist die Steigung doppelt so hoch, ist auch die Amplitude doppelt so hoch
- Ist die Steigung nur halb so hoch, ist auch die Amplitude halb so hoch
- Braucht die Schwingung doppelt solang, ist auch die Amplitude doppelt so hoch
- ...
Fehlt noch der Faktor, wie umrechnen. Der ist noch trivialer, es ist nämlich derselbe Faktor wie zwischen Radius und Umfang eines Kreises: 2 Pi r = U.
Amplitude = ( Periodendauer / 2 Pi ) * (Hebungswinkel / Länge des Ticks)
Sehen wir noch mal unser Beispiel daraufhin an:
Amplitude = ( 250 ms / 2 Pi ) * ( 50° / 10 ms ) = 39,8 ms * 5 °/ms = 199°
Bingo!
Disclaimer:
Die Grafiken sind nicht massstäblich, die Diagramme schon.
Das dem gezeigten Anker zugrunde liegende Bild stammt von einem ETA 775x Anker.
Die Formel ist idealisiert, sie berücksichtigt werde die Reibung, die die Schwingung abbremst, noch den Impuls, der die ganze Form etwas verdrückt. Sie gälte genau genommen auch nur wenn man die Steigung als Grenzwert gegen Null ermitteln würde, mit unendlich kleinem Hebungswinkel. Auf der andern Seite, so genau kommt es auf die Amplitude auch gar nicht an, 10° Grad hin oder her, da braucht man sich absolut keinen Kopf drum machen. Ausserdem ist es in der Realität gar nicht so einfach ganz genau festzustellen, wie lange der Tick ist, das Mikrophon, die Umgebung, der Verstärker, alles rauscht die ganze Zeit fröhlich mit. Da muss man für eine professionelle Zeitwaage eh noch mal extra Aufwand reinstecken, da würde eine genauere Formel auch keine relevante Verbesserung bringen.
Wo die Formel dann doch deutlich abweicht, wenn die Amplitude nicht mehr grösser als der Hebungswinkel ist. Nur, dann versagt auch die Hemmung selber, physisch und real, also auch nichts, was eine aufwendigere Modellierung der Berechnung rechtfertigen würde.